Variety of “Shape” Notions

With advancements in areas of technology, such as digital manufacturing, computer graphics, digital scanning, social networks, computer vision, and machine learning we find a variety of “shape” notions, including point-sets as “noisy” signals, networks or graphs of interconnected nodes (e.g., molecules in computational biology or nodes in social networks), unstructured point-clouds, discretized representations (e.g., triangle meshes), vector graphics, and other. Each approach to shape carries its own mathematical framework, including its own algebra (where operations such as + or – are defined), geometry (where transformations are defined), and topology (where structural relations are defined). Which approach to shape to use depends each time on the notion of shape adopted in an application, and decisions of this kind influence how shapes are represented and which operations are, or are not, possible or computationally efficient.

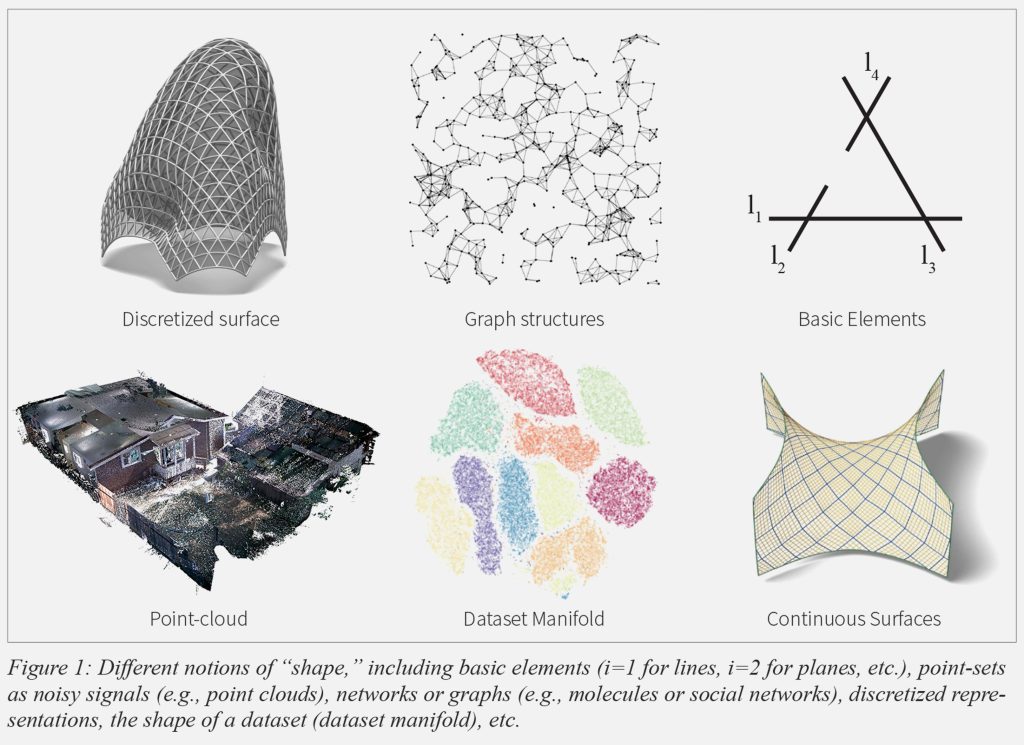
Mathematics of Shape

In a series of articles (see below), my work contributes new results in the area of mathematics of shape as it appears in the computational design theory of shape grammars. Among the various topics of research that have emerged over the past decades, the following three relate to my work:

(a) The algebras of shapes U_i, defined according to the dimensionality i of basic elements (i = 0 for points, i = 1 for lines, i = 2 for planes, i = 3 for solids).

(b) Structural descriptions, such as finite topologies and other decompositions (e.g., Haridis 2020; Haridis and Stiny 2022; Krstic 1996).

(c) Algorithmic features of computations with shapes that distinguish them from computations with models of computation (e.g., Turing machines, Phrase Structure Grammars, Markov algorithms).

In architecture and spatial design, the practicality and intuitiveness of working with higher-level primitives – such as lines, polygons, surfaces or other shapes – is evident in the visual/physical basis of the calculational work of Gothic masons, the use of “force polygons” in form-finding in structural design with graphic statics, the “algebras of design” in shape grammars, and in the empirical use of drawings, physical models, and other graphic representations in the architectural practice and in studio teaching. My work on mathematics of shape seeks to establish a more natural, spatial framework for studies on the mathematical structure of design objects in architecture, or art and design. It shows, more generally, how mathematical constructs (e.g., topology) can be built directly in terms of visual-spatial objects as opposed to the more common, opposite approach where these objects are subjugated to canonical constructs (e.g., point-sets).

Topology and Continuity

Traditionally, the objects upon which one confers a topology are represented as point-sets, in one space or another (Kuratowski 1972). In general topology (point-set topology), topologies for shapes are modelled after the classical concept of “topological space” (Munkres 2000): a shape is considered a subspace of an underlying ambient space (e.g., Euclidean space), which possesses a set of points and a predefined system of subsets containing the points; the subsets determine “relations” between points in continuous (a) or discrete spaces (b).

The point-set view allows for transferring constructions from the existing literature of mathematical topology to the study of topology for shapes in design domains. This approach is followed, for example, in morphological studies in architecture and in engineering design of products (Rosen & Peters 1996), with techniques analogous to classificatory studies concerning knots, braids and links, surfaces and simplicial complexes (Lefschetz 1942; Munkres 2000). Most notably, it is the basis for geometric modeling in computer graphics and Computer-Aided Design.

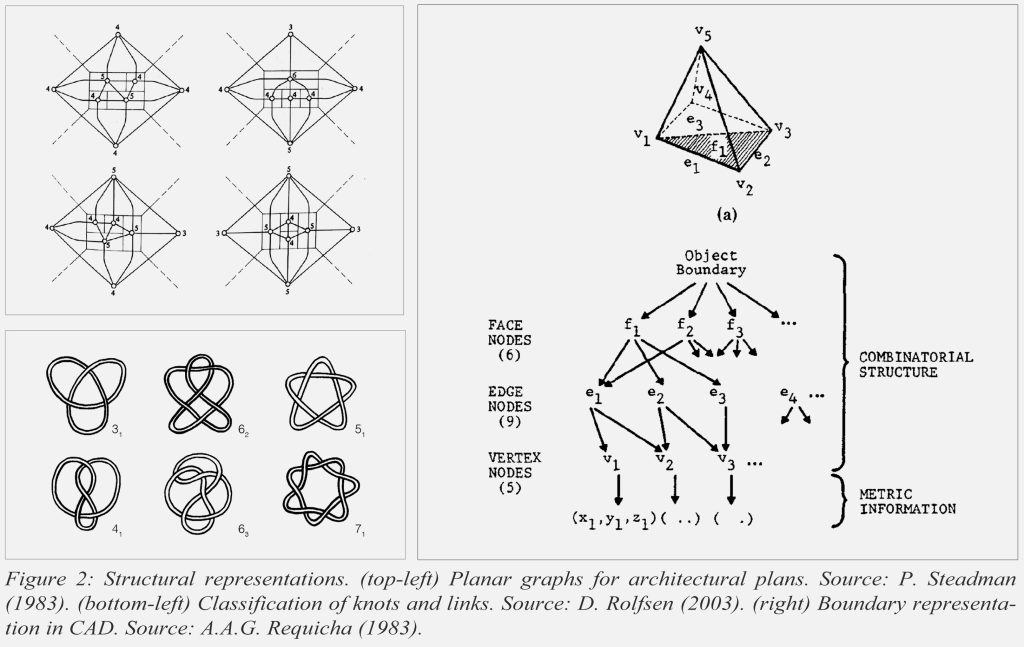
In contrast to point-set representations, alternative systems have been proposed based on higher-level primitives (i.e., without recourse to points of dimension i = 0). In philosophy and mathematics, examples include the concepts of “solid and contact” (Lobachevsky), “regions” and “connection relations” (Whitehead), or “individuals” (Leonard and Goodman). Such systems are used to contemplate the natural processes and time events governing the behavior of physical bodies, but have also inspired modern developments in category theory, functional programming, and robotic vision (e.g., for grasping and interpreting spatial configurations in context).

My research work has developed shape topology, a framework for assigning topological structures on shapes in the algebras Ui where shapes are defined in a point-free manner. In this framework, an interpretative, aesthetic dimension is introduced in the sense that “topological structure” is not inherited from a predefined ambient space, but is induced based on how a shape is interpreted into parts. Basis, continuity, connectedness, and other foundational topological concepts, are formulated directly in terms of shape and topological structures defined by parts. In the absence of a point-set substrate, topological concepts normally defined in terms of points are formulated in terms of part relations and their formulation is driven by pictorial and spatial concepts.

This approach to topology provides a natural grounding to design-inspired processes. Shape topology also assimilates structure-oriented theories of human perception originating from AI and cognitive psychology that focus on characterizing higher-level outcomes of the human perceptual process (e.g., part-whole grouping, hierarchical decomposition) as opposed to lower-level neurocognitive process mechanisms (e.g., how brain regions are activated and why, how complex patterns are synthesized by low-level features). Shape topology also makes topological concepts accessible to designers, engineers, or mathematics students from the perspective of visual/physical objects. This provides a formal way of investigating design-inspired topics such as structural change, continuity, and design innovation.

Related Work

This portfolio item is based on the following three publications:

(1) The journal article “Structure from appearance: topology with shapes, without points” (Journal of Mathematics and the Arts, Vol. 14) describes a point-free topological approach to the topology of two and three-dimensional shapes

(2) The journal article, “The topology of shapes made with points” (Environment and Planning B, Vol. 47), establishes the correspondence between the topology of finite discrete sets and the topology of shapes made with point-like elements (when dimension i=0)

(3)  The book chapter, “Arrangements containing shapes: mathematical features and their use in visual calculating” (Mathematics and the Built Environment Book Series, Vol. 9), describes the properties of hyperplane arrangements in the plane that contain shapes made with lines (dimension i=1) and their use for shape computations

(4) The journal article, “Analysis of shape grammars: continuity of rules” (Environment and Planning B, Vol. 49), describes how shape topology can be applied to the analysis the rule continuity of a computation with shape grammars where every new rule application reconfigures the computation history, i.e., the shape topologies that have been generated in previous rule applications